Wir verwenden in unserem Tool eine Prognose auf Basis eines gleitenden Durchschnitts. Bisher arbeiten wir dabei mit dem arithmetischen Durchschnitt der letzten vier (dynamisch) oder sieben (stabilisiert) Tage [Im Folgenden bezeichnen wir diese Methode als arithmetische Wachstumsrate]. Dieser ermöglicht uns, (stärker) unabhängig von der regionalen Entwicklung Prognosen auch für einzelne Gebiete zu berechnen. Wir modellieren also für jede Region auf Basis der tatsächlichen Fallzahlen. Aufgrund des Feedbacks eines Anwenders wollen wir auch prüfen, ob wir zukünftig den geometrischen Durchschnitt für beide Wachstumsraten nutzen [Im Folgenden bezeichnen wir diese Methode als geometrische Wachstumsrate].
Für die nationale Entwicklung (und damit für die Prognose auf Basis des Bevölkerungsanteils sowie alle Prognosen auf Basis der bundesweiten Wachstumsrate) müssen wir zusätzlich andere Wachstumsprognosen prüfen. Insbesondere die bereits erläuterte logistische Wachstumsrate, die sich in epidemiologischen Simulationen als prognostizierte Entwicklung zeigt, könnte für die mittel- bis langfristige Prognose von zentraler Bedeutung sein. Wir haben daher auf Basis der Fallzahlentwicklung eine Modellierung mit den verschiedenen Methoden vorgenommen und die jeweils prognostizierten Fallzahlen mit den tatsächlichen Zahlen abgeglichen. An dieser Stelle muss betont werden, dass durch die unzureichende Datenbasis ein wirklicher Abgleich natürlich keine Beweiskraft hat, sondern nur Hinweise auf die tatsächlichen Zusammenhänge bieten kann.
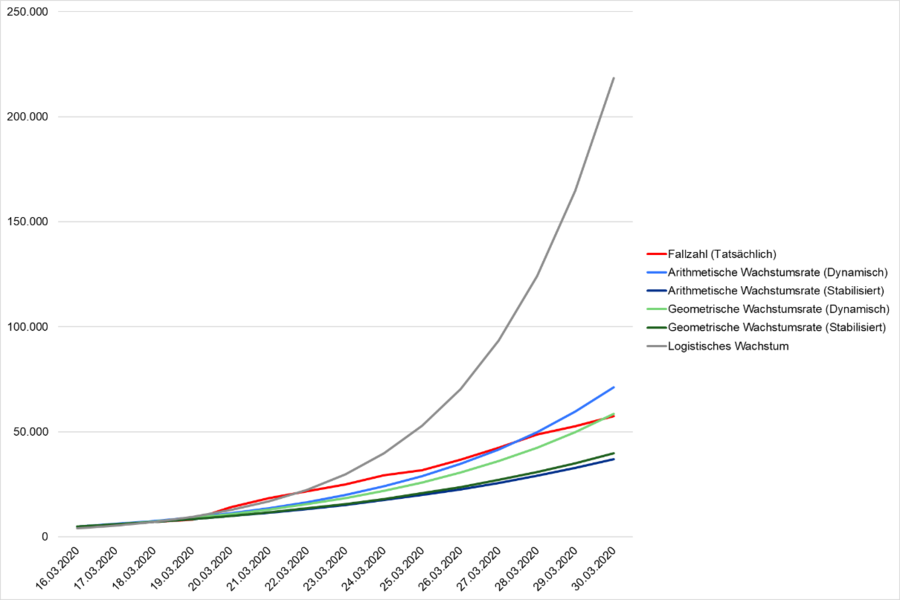
Abbildung 10 zeigt den Vergleich der jeweiligen Prognosen mit den tatsächlichen Fallzahlen (rot). Grundlage der jeweiligen Prognosen sind die Daten vom 26. Februar bis zum 16. März. Die Prognose erfolgt jeweils bis zum 30. März. Deutlich zeigt sich, dass die Entwicklung in diesem Zeitraum von der geometrischen dynamischen Wachstumsrate am besten prognostiziert wurden. Die Wachstumsprognose der letzten Tage wird allerdings deutlich überschätzt. Es scheint, als ob der Fallzahlzuwachs stärker zurückgeht als zu erwarten gewesen wäre. Die logistische Wachstumsrate liegt deutlich über den tatsächlichen Fallzahlen.
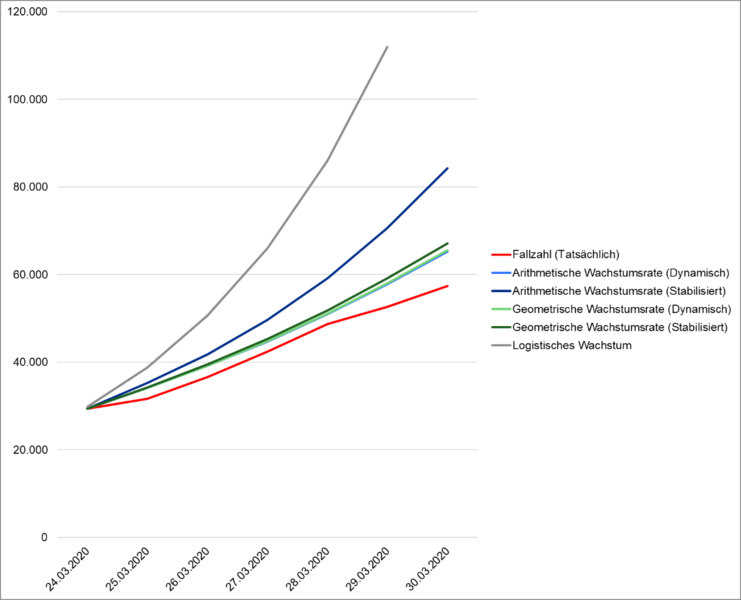
Mit größerer Datenbasis ändert sich die jeweilige Vorhersagekraft. Dafür haben wir denselben Vergleich mit größerer Datenbasis (alle Fallzahlen bis einschließlich 24. März) durchgeführt. Abbildung 11 zeigt die ersten Ergebnisse.
Hier zeigen sich weniger starke Unterschiede zwischen den Prognosemethoden. Alle Methoden überschätzen die tatsächlichen Fallzahlen, wobei das logistische Wachstum die mit Abstand größte Überschätzung zeigt. Dabei ist wichtig zu beachten, dass die einbezogenen Vergleichsdaten noch sehr gering sind – wir prüfen lediglich die Prognose der folgenden sechs Tage. Noch können wir nicht sagen, ob sich die langfristige Prognose mithilfe der logistischen Wachstumsrate verbessert oder nicht. Die bisher im Rechner verwendeten arithmetischen Wachstumsraten zeigen ordentliche Prognoseergebnisse. Dabei sind die Vorhersagen auf Basis der stabilisierten Wachstumsrate allerdings deutlich höher. Das zeigt uns: Das Wachstums der Infektionen ist aktuell weniger stark, als befürchtet. Vielleicht greifen die gesellschaftlichen Maßnahmen bereits, die sich (kurzfristig) nur in der dynamischen Rate widerspiegeln. Deutlich erkennen wir auch, dass die geometrische Wachstumsrate bessere Prognoseergebnisse liefert.
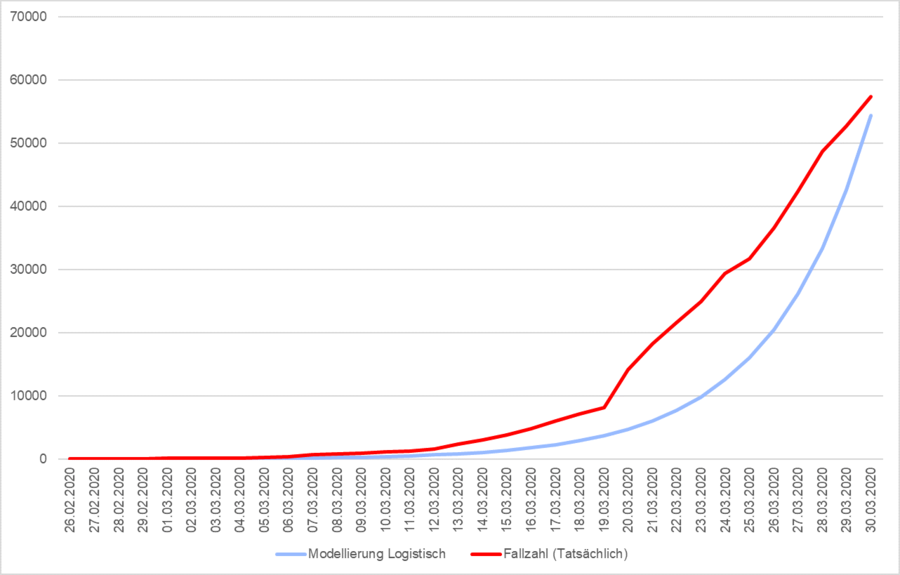
Um die logistische Wachstumsrate einer genaueren Prüfung zu unterziehen, betrachten wir die Modellierung des bisherigen Verlaufs. Abbildung 12 zeigt die tatsächlichen Fallzahlen im Vergleich mit dem modellierten Verlauf. Besonders auffällig ist der steile Anstieg der modellierten Rate an den letzten betrachteten Tagen, die sich in den Zuwächsen der letzten Tage eher nicht andeutet. Zum Vergleich ziehen wir unsere europäischen Nachbarländer heran.
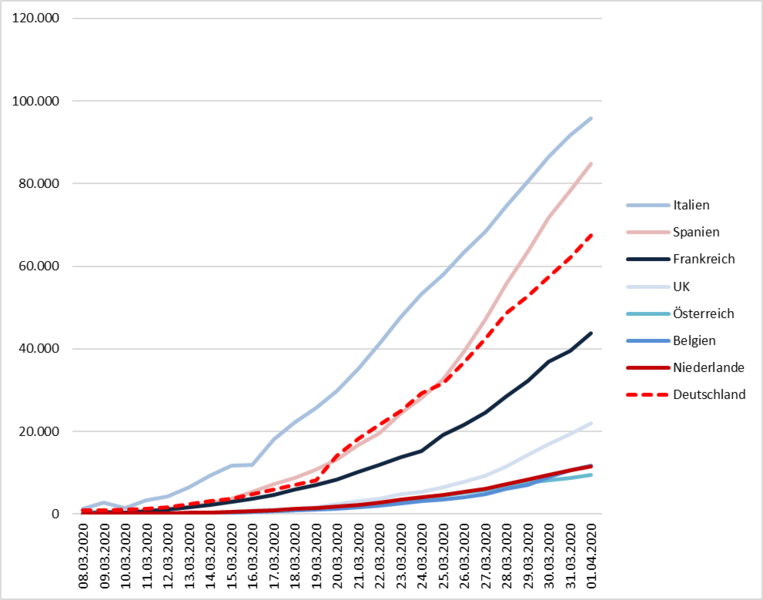
Wir erkennen die charakteristische Zunahme der Fallzahlen und der Wachstumsrate ähnlich wie in Deutschland. Auffällig ist aber, dass die Wachstumsrate in vielen Ländern aktuell stagniert oder sogar etwas zurückgeht. In Italien beispielsweise liegt der absolute Zuwachs pro Tag seit dem 12. März (fast) immer bei 4.500 bis 5.500 Fällen; es zeigt sich ein fast linearer Verlauf der kumulierten Fallzahlen. Betrachtet man die letzten beiden Tagen, ist die Wachstumsrate sogar leicht rückläufig (jeweils etwa 4.000 neue Fälle). Die italienische Wachstumskurve ähnelt stark der deutschen, sodass wir für unsere Prognose eventuell Rückschlüsse aus ihr ziehen können. Die spanische Wachstumskurve ist signifikant steiler als in anderen europäischen Ländern, während sich die kleineren europäischen Nachbarländer (Österreich, Belgien, Niederlande) noch mit ähnlichen Wachstumsraten auseinandersetzen müssen. Je kleiner die betrachtete Einheit, desto unklarer der tatsächliche Verlauf der Pandemie. Für unsere Prognosemethodik ist das äußerst relevant, da wir bestmögliche Prognosen auch auf regionaler Ebene anbieten wollen. Mit einer einfachen Modellierung anhand einer logistischen Wachstumsrate scheint es dabei nicht getan. Wir sehen also wiederum das vielschichtige, hochkomplexe Zusammenspiel verschiedener Faktoren; die Schwierigkeit der (langfristigen) mathematischen Modellierung wird deutlich.
Zentrale Erkenntnis des Vergleichs ist, dass wir aktuell nur Momentaufnahmen betrachten (können). Jede neue Erkenntnis führt zu einer besseren Prognose. Unsere Vorgehensweise, den Rechner täglich zu aktualisieren und die Prognosemethoden auf Basis der tatsächlichen Fallzahlentwicklung immer wieder zu hinterfragen, wird durch diesen Vergleich gestärkt. Auch die Anwender sollten daher das tägliche Update betrachten und Veränderungen zum Vortag hinterfragen. Die Frage, ob eine logistische Wachstumsrate für den Anwender bessere Prognosedaten liefert, können wir noch nicht endgültig beantworten.
Im nächsten Beintrag unserer Blogreihe widme ich mich der Datenbasis, auf der unsere Berechnungen beruhen, sowie der Frage: Wie weit in die Zukunft können und sollten wir denken?
Lesen Sie hier weiter »Teil 5: Die Qualität der Datenbasis: Worauf basieren die Prognosen?